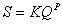 (2.1)
(2.1)
2.3 方法
2.3.1 HYCYMODEL
1) HYCYMODELの構造
水分貯留量と流出量の間の次式の関係が一般にタンクモデルにおいて用いられる。
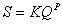 (2.1)
(2.1)
ここで、Sは貯留量、Qは流出量、KとPはパラメータである。P=1.0のとき、SとQの関係はリニアであり、P≠1.0のとき、その関係はリニアではない。
図-2.4に示すように、HYCYMODELは5つの貯留タンク(I-V)を持つ。長方形のタンクはリニアシステム(P=1.0)を示し、上端が開いているタンクは非リニアなシステム(P≠1.0)を示す。非リニアなシステムの内、直接流出に関するタンクIVとタンクVでは、Manning則と同一のP=0.6を用いることによって良好な近似が得られることが指摘されている(角屋ら, 1987; 福嶌・武居, 1981)。また、タンクIIIでは、福嶌・鈴木(1986)と同様にP=0.1とする。

図-2.4 水循環モデル(HYCYMODEL)の模式図
Concept of the hydrologic cycle model(HYCYMODEL)
降雨R(t)は、流出Q(t)と各サブシステムを通して起こる蒸発E(t)に寄与する。R(t)は、パラメータCによって、不透水帯としての流路システムと、透水帯としての斜面システムに入力される(図-2.4)。パラメータCは、不透水帯の占める面積的な割合を表現し、0から1の値をとる。流路システムにおいては、流路降雨Rc(t)(=R(t))が貯留量Sc(t)を持つタンクVに入力される。タンクVの出力が流路からの直接流出(流路直接流出)Qc(t)である。流路直接流出における単位流域面積当たりの水量(水深当量)Qc*(t)は、次式で表される。
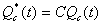 (2.2)
(2.2)
斜面システムにおいては、総降雨Rg(t) (=R(t))が、一部はタンクIにおいて遮断され、地上到達降雨Rn(t)が、タンクIから溢れ落ちる。Rn(t)は、タンクIIへ入力される。タンクIIの貯留量Su(t)は、次式によって計算される。
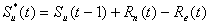 (2.3)
(2.3)
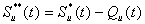 (2.4)
(2.4)
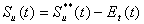 (2.5)
(2.5)
ここで、Re(t)は斜面からの直接流出のための有効降雨である。Re(t)を算出するための方法は後に述べる。Qu(t)はタンクIIからタンクIIIへの土壌水の浸透である。Et(t)は植生による蒸散である。Re(t)は貯留量Sh(t)を持つタンクIVに加えられ、斜面からの直接流出(Qh(t))に変換される。斜面からの直接流出の水深当量Qh*(t)は次式で表される。
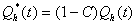 (2.6)
(2.6)
したがって、全直接流出Qd(t)は、次式で表される。
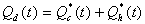 (2.7)
(2.7)
土壌水の一部は、主に森林表層土壌から植物の根により吸水され、蒸散によって大気中へ戻る。そこで、蒸散量Et(t)が森林表層土壌における空隙を表すタンクIIから差し引かれる。タンクIIIはタンクIIの下に配置され、毛管によって連結される。タンクIIIは森林土壌の微細空隙を表す。基底流出Qb(t)は、Qu(t)がタンクIIIにおける貯留Sb(t-1)に加えられた後に算出される。Sbcは、乾燥ストレスによる蒸散抑制を引き起こす限界貯留量である。流路からの蒸発Ec(t)は、全ての流路流出が流路に集まった後に起こる。対象流域における基底流出の水深当量Qb*(t)は次のように定義される。
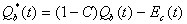 (2.8)
(2.8)
したがって、全流出Q(t)は、次式となる。
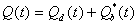 (2.9)
(2.9)
2) 遮断蒸発モデル
タンクIの構造は既に図-2.5のようにモデル化されている(鈴木ら、1979)。樹冠を表す貯留量S1を持つタンクが全降雨Rg(t)によって満たされた後、越流が地表と樹幹を表すもうひとつのタンクへ、その割合a1およびa2に応じて、それぞれ分配される。樹幹からの越流は、貯留量S2を満たした後、地表へと達する。両方のタンクに降雨水が残っている時は、蒸発強度は、ei mm/hrである。地上到達降雨Rn(t)は、両タンクからの越流である。遮断蒸発Ei(t)は、次式で表される。
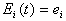 (if
(if 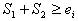 ) (2.10)
) (2.10)
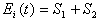 (if
(if 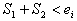 ) (2.11)
) (2.11)
また、水深当量Ei*(t)は次式で表される。
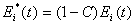 (2.12)
(2.12)

図-2.5 遮断蒸発モデル
Interception model
3) 蒸散モデル
福嶌(1987)は、同一地域における蒸散量の季節変化の年格差は、気象要因の変化に伴い気孔開閉を調節することによって樹木が蒸散を制御するので、蒸発量の年格差に比べて、微少とみなせるとしている。ただし、土壌水分が欠損する条件下では、蒸散速度は低下すると考え、十分な土壌水分がある条件下での蒸散の季節変化をポテンシャル蒸散量ep(i)と与えている。ここで、iは月である。
タンクII、タンクIIIの両タンクに貯留がある場合、実際の蒸散量Et(t)の推定には、次の3通つの式が適用される。
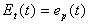 (if
(if 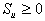 ) (2.13)
) (2.13)
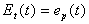 (if
(if 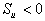 and
and 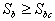 ) (2.14)
) (2.14)
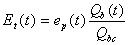 (if
(if 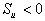 and
and 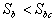 ) (2.15)
) (2.15)
ここで、 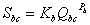 であり、Sbcは土壌水分欠損の限界点である。(2.15)式は蒸散速度が土壌水分欠損ストレスによって減少することを表している。
であり、Sbcは土壌水分欠損の限界点である。(2.15)式は蒸散速度が土壌水分欠損ストレスによって減少することを表している。
第1の場合((2.13)式)、Et(t)はep(I)に等しく、蒸散は、(2.5)式によってSuの水を消費する。(2.14)式において、タンクIIにおける蒸散による欠損は、タンクIIIから毛管を通して水が供給されることにより、素早く回復する。見かけ上、蒸散は次のように起こる。タンクIIでは、(2.5)式の変わりに次式を用いる。
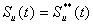 (2.16)
(2.16)
また、タンクIIIでは、次式を用いる。
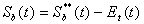 (2.17)
(2.17)
ここで、
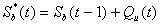 (2.18)
(2.18)
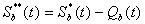 (2.19)
(2.19)
である。
第3の場合((2.15)式)、蒸散速度は、毛管の部分的な断絶に従って減少する。毛管が途切れるため、第3の場合の蒸散もまた(2.5)式を用いて、タンクIIから引き起こされる。したがって、この場合には、Suはゼロ以下へ徐々に減少する。蒸散の水深当量Et*(t)は次式で表される。
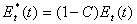 (2.20)
(2.20)
4) 流路面蒸発モデル
流路面における蒸発の季節分布が与えられれば、その面積に応じて流路面蒸発Ec(t)が定まる。その分布をポテンシャル蒸散量の季節分布で近似し、次式より算出する。
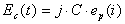 (2.21)
(2.21)
ここで、jは、補正のためのパラメータであり、福嶌・鈴木(1986)、中島ら(1992)と同様にj=2.0とする。
5) 直接流出に寄与する有効降雨のモデル
有効降雨を算出するモデルは、福嶌ら(1984)によって提案されている。土壌深度の空間分布は、対数正規分布によって表現される(窪田ら, 1983)。一方、表層土の空隙率が直接流出に関わる(Takeshita and Takagi, 1977)。表層土中の鉛直方向に積算された空隙の空間分布もまた、対数正規分布で表現できる仮定すと、ある深度以下表層土における空隙率は、積分計算によって得られる。降雨水によって、それらの空隙が満たされる時、直接流出が起こるものとする。
有効降雨Re(t)は、タンクIIの貯留量Su(t-1)と、地表到達降雨Rn(t)の両者によって決定され、モデル中では、(2.22)〜(2.25)式によって表現される。D16およびD50を、それぞれ、有効降雨発生率mが、16%および、50%となる有効土層深として定義すると、標準偏差sは、次式で表される。
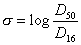 (2.22)
(2.22)
有効降雨発生率mは、次式で表される。
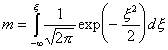 (2.23)
(2.23)
ただし、変数xは次式で表わされる。
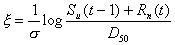 (2.24)
(2.24)
したがって、
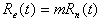 (2.25)
(2.25)
ここで、Suがゼロ以下の時、地上到達降雨Rn(t)はSuをゼロに回復させるのに使われる。そのような状況は、乾燥の直後に雨が降った時に有効降雨発生率mが減少するという現象についてのモデル上での表現である。このように、Suは、蒸散と有効降雨の両者に関係している。
同様の定式化は、Sharma and Luxmore(1979)によって提案され、土壌の空間多様性を考慮する目的で用いられている。