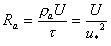 (4.7)
(4.7)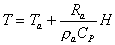 (4.8)
(4.8)
4.3.2シミュレーションの結果
光合成および、蒸散が活発に行われてたと考えられる夏期の1998年6/8-7/23の期間の観測データを用いて第3章で記述したモデルによるCO2およびH2Oフラックスの再現計算を行った。ただし、空気力学的抵抗Raおよび仮想葉温度Tは、風速(U)、気温(T)、運動量フラックス(u*2)、顕熱フラックス(H)より、次式を用いて算出したものを用いた。
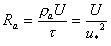 (4.7)
(4.7)
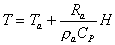 (4.8)
(4.8)
群落抵抗サブモデルおよび光合成サブモデル中の各森林毎に決定されるべき未知パラメータは、それぞれ、計算される潜熱フラックスおよびCO2フラックスと、観測されたものとの残差平方和が最小となるように、非線形回帰分析を用いた最適化手法によって決定した。表-4.1に最適化されたパラメータを示す。ただし、群落抵抗サブモデルにおける、仮想葉温度の変化が群落抵抗に与える影響を表す関数gは、第3章と同様に、仮想葉温度の変化による群落抵抗への影響が非線形回帰分析の結果、検知されなかったため、g(T)=1.0とした。
表-4.1 シベリアタイガ・カラマツ林において見積もられたパラメータ
Estimated parameters in Larix forest, Siberian Taiga(1998/6/8-7/23)
| Parameter | Value |
| Rcmin | 43.75 |
| a | 0.00001053 |
| Tx | - |
| To | - |
| Tn | - |
| b | 0.02697 |
| r | 0.3756 |
| Rd25 | 0.05629 |
| e(1-f) | 0.07406 |
群落抵抗と、日射量、仮想葉温度、飽差との関係を図-4.15a,b,cに示す。実線は、群落抵抗サブモデルにおいて、最適化された関数を表す(第3章参照)。Rcmin/Rc-Q曲線(関数f)は、PARの増大に対する立ち上がりが、PARが2000 mmol m-2 s-1においても0.5程度と、第3章で示した暖温帯のヒノキ林に比べて小さいことが分かる。図-4.15cでは、第3章で示した暖温帯ヒノキ林におけるものと同様に、実際のRcmin/Rcが0から関数hの間にほぼ均一に分布しており、様々な環境下で、 Rcmin/Rcは変化し、飽差の影響を受けていることが示唆される。
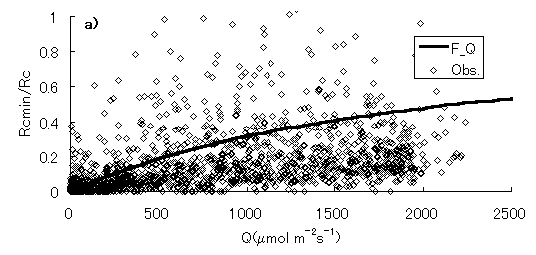
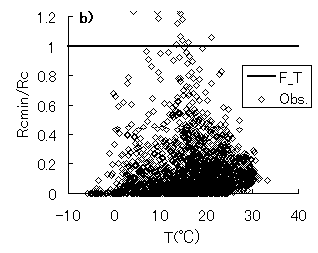
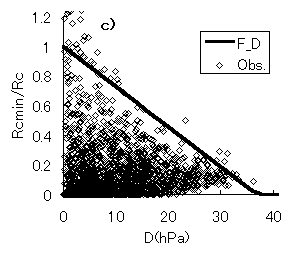
図-4.15 群落抵抗(Rc)と、光合成有効放射量(Q)、仮想葉温度(T)、飽差(D)の関係(a: Rc-Q, b: Rc-T, c: Rc-D)
Relationships between canopy resistance(Rc) and PAR(Q), canopy temperature(T) and vapor pressure deficit(D),
(a: Rc-Q, b: Rc-T, c: Rc-D)
表-4.1に示したパラメータ群は、光合成・蒸散速度の環境応答特性が大きく変化しないと予想される夏期(1998年6/8-7/23)の観測データによって最適化されたものである。春期(1998年5/15-6/7)および秋期(1997年8/17-8/30)では、これらの応答特性が夏期とは大きく異なると予想される。そこで、これらの期間についても表-4.1に示したパラメータ群を用いて、H2OおよびCO2フラックスの再現計算を行い、観測されたフラックスとの比較を行った。モデルによる潜熱・CO2フラックスの算出結果を、観測で得られたフラックスとともに図-4.16および図-4.17に示し、群落抵抗の変化を図-4.18に示す。また、図-4.19に、5日平均されたフラックスおよび群落抵抗の日変化の推移を示す。
図-4.16 パラメータを一定とした場合の計算された潜熱フラックスの変化 Change in latent heat flux calculated with constant parameters
図-4.17 パラメータを一定とした場合の計算されたCO2フラックスの変化 Change in CO2 flux calculated with constant parameters
図-4.18 パラメータを一定とした場合の計算された群落抵抗の変化 Change in canopy resistance calculated with constant parameters
図-4.19 パラメータを一定とした場合の5日平均された潜熱フラックス、 CO2フラックス、群落抵抗の日変化の推移 Variation in mean diurnal change for 5 days of latent heat flux, CO2 flux and canopy resistance calculated with constant parameters
潜熱フラックスは、展葉終了以前の春期についても、計算値が観測値に、よく一致する。しかしながら、蒸散速度を支配する群落抵抗は、計算値が観測値よりも過小に算出された。展葉終了以前には、気温が低く飽差が小さいため、群落抵抗の違いよる潜熱フラックスの推定誤差が小さかったものと考えられる。CO2フラックスは、計算値が非常に大きく見積もられた。森林群落の蒸散・光合成速度の環境応答特性は、展葉終了の前後で大きく変化し、一致しなかったと考えられる。
そこで、これをより詳細に明らかにするため、観測が行われた全期間を、サンプル数が少なくとも100程度となるように、1997/8/17-8/26、8/27-8/30、1998/5/15-5/30、5/31-6/3、6/8-6/10、6/11-6/13、6/14-6/21、6/22-7/2、7/3-7/14、7/16-7/23の10区間に分けて、群落抵抗サブモデルおよび、光合成サブモデルにおいて、それぞれ、最小群落抵抗(Rcmin)および、クロロフィル密度(r)と光量子吸収率(e(1-f))に着目し、以下のように、区間毎のそれらの最適値を見積もった。
区間毎にパラメータを最適化する場合、それぞれの区間における気温および飽差の変化幅が小さいため、全てのパラメータを同時に最適化することは困難である。そこで、群落抵抗サブモデルでは、比較的季節変化の小さいと考えられるサブモデル中のRcmin以外のパラメータ(a、Tn、To、Tx、b)を、便宜上、表-4.1に示したものに固定し、各区間において観測されたH2Oフラックスと計算されるものの残差平方和が最小となるRcminを求めた。得られたRcminを用いて、区間毎に群落抵抗およびH2Oフラックスを算出する。次に、光合成サブモデルにおいて、Rd25を便宜上、表-4.1中の値をそのまま用いて、各区間で観測されたCO2フラックスと計算されるフラックスの残差平方和が最小となるrおよびe(1-f)の組み合わせ求めた。このように求められたパラメータを用いて算出されたCO2およびH2Oフラックスと群落抵抗は、全期間を通じて観測によって得られたフラックスおよび群落抵抗と良好に一致する。図-4.20〜図-4.22に計算されたフラックスおよび群落抵抗の変化を観測されたものとともに示す。また、図-4.23に5日平均のフラックスおよび群落抵抗の変化を示す。
図-4.20 パラメータを季節変化させた場合の計算された潜熱フラックスの変化 Change in latent heat flux calculated with seasonal varied parameters
図-4.21 パラメータを季節変化させた場合の計算されたCO2フラックスの変化 Change in CO2 flux calculated with seasonal varied parameters
図-4.22 パラメータを季節変化させた場合の計算された群落抵抗の変化 Change in canopy resistance calculated with varied parameters
図-4.23 パラメータを変化させた場合の5日平均された潜熱フラックス、 CO2フラックス、群落抵抗の日変化の推移 Variation in mean diurnal change for 5 days of latent heat flux, CO2 flux and canopy resistance calculated with seasonal varied parameters
以下では、季節的に変動するパラメータについてその変動の特徴を検討する。
1) 最小群落抵抗(Rcmin)
群落抵抗サブモデル中のパラメータである最小群落抵抗Rcminは、仮想葉における気孔の開度を表すパラメータである群落抵抗(Rc)の最低値である。このため、Rcminが大きければ、気孔は開きにくく、蒸散および光合成が抑制される。つまり、Rcminは、仮想葉の気孔開閉を表すが、群落の場合、個々の葉の気孔開閉などの特性が複合的に影響する。図-4.24にRcminの変化を示す。Rcminは、5月には非常に大きく、6月初旬に急激に低下した。これは、図-4.2に示したLAIの急激な変化の時期と一致し、開葉による影響と考えられる。その後、6月下旬から7月中旬までの間、ほぼ一定の値を保ち、7月中旬以降、増大した。
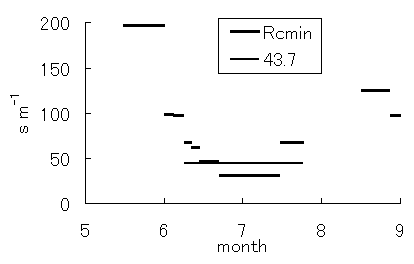
図-4.24 最小群落抵抗(Rcmin)の季節変化
Seasonal variation of minimum canopy resistance(Rcmin)
開葉期におけるRcmin低下は、葉量の変化によると考えられ、7月中旬以降のRcminの増加は、葉の老化によるものと考えられる。開葉完了後もしばらくの間Rcminはゆるやかに低下を続けていることから、気孔開閉に関する機能が十分に発達するまでには、時間がかかることが示唆される。本対象森林では、定常状態に達するまでの時間は、14日程度と見積もられた。
2) クロロフィル密度(r)、光量子吸収率(e(1-f))
光合成サブモデル中のパラメータであるクロロフィル密度(r)および、光量子吸収率(e(1-f))は、葉の光合成特性を示すパラメータである。図-4.24a,bにrとe(1-f)の変化を示す。5月には両者とも、ほとんどゼロとなり、6月初旬に急激に増加した。これは、Rcminの変化と同様にLAIの急激な増加の時期と良く一致する(図-4.2参照)。その後、rは、ほぼ一定の値を維持し、8月末に低下した。一方、e(1-f)は、その後もしばらく増大し、7月初旬より緩やかに低下した。
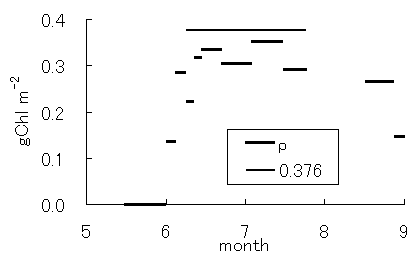
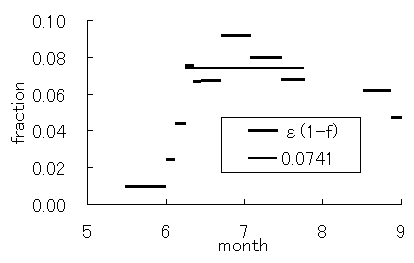
図-4.25クロロフィル密度(r)および光量子
吸収率(e(1-f))の季節変化(a: r, b: e(1-f))
Seasonal variation of the density of chlorophyll(r)
and the fraction of the incident PAR available
for PCR/PCO cycles(a: r, b: e(1-f))
概念的には、rは、仮想葉中のクロロフィル密度を表し、群落においては、葉量あるいは葉面積と密接な関係があるものと考えられる。このことは、開葉期におけるLAIの変化とrの変化に良い一致が見られることからも推察される。一方、e(1-f)は、仮想葉に届いたPARの光合成における有効吸収率であり、群落においては、個々の葉におけるPARの反射・吸収率、葉緑体におけるPAR有効吸収率、森林群落の幾何学的な構造などが複合的に影響すると考えられる。