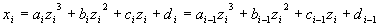
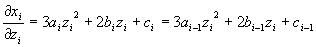
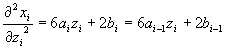
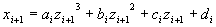
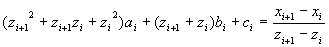
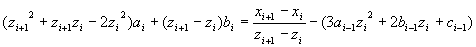
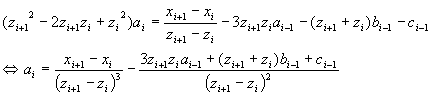
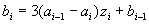
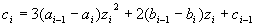
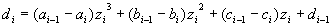
t	z	x
---	---	---
1	z1	x1
			} x = a1z3 + b1z2 + c1z + d1
2	z2	x2
			} x = a2z3 + b2z2 + c2z + d2
3	z3	x3
・	・	・
・	・	・
			} x = ai-1z3 + bi-1z2 + ci-1z + di-1
i	zi	xi
			} x = aiz3 + biz2 + ciz + di
i+1	zi+1	xi+1
・	・	・
・	・	・
			} x = an-1z3 + bn-1z2 + cn-1z + dn-1
n	zn	xn

というn組の (x_i, z_i)があるとき、 それぞれの区間を x = a_iz³ + b_iz² + c_iz + d_i のような３次関数で表現し、各点をn-1個の曲線でつなぐものとする。 この時、各点での傾きおよび曲率を連続的にしたものをspline関数という。 すなわち、以下の条件を満たす。

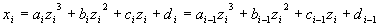		(1)
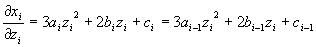		(2)
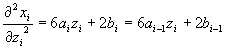		(3)
これに、次	式を加えれば、 ai,bi,ci,di についての漸化式ができる。
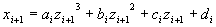		(4)
(1)(4)より
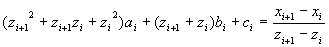		(5)
(2)(5)より
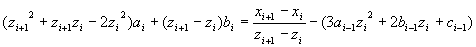		(6)
(3)(6)より
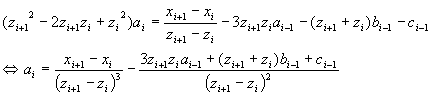		(7)
であり、(3)	(2)(1)より
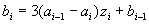		(1)
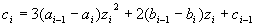		(2)
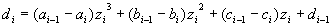		(3)
と、次々に	求まる。

ただし、この漸化式を解くためには 初期値(a₀,b₀,c₀,d₀)が必要である。
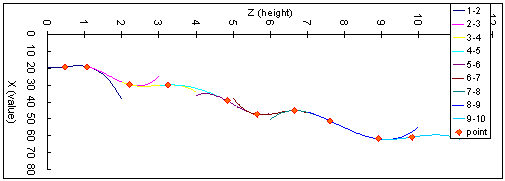
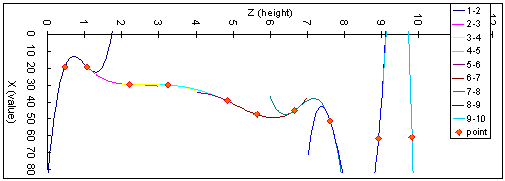
適切な初期値を設定しない場合、各点間の曲線は 大きく振れる可能性もある。 特に、この漸化式を用いて順次導いていくと、tが大きくなるに連れて、勾配および曲率が発散していく 傾向があるようだ。とりあえずは、 t=n地点でのd²x/dz²の絶対値が最小となるように初期値を決めると 比較的ブレが小さくなるようだ。 きっと、もっといい方法はあるに違いないが、今のところはこんな認識である